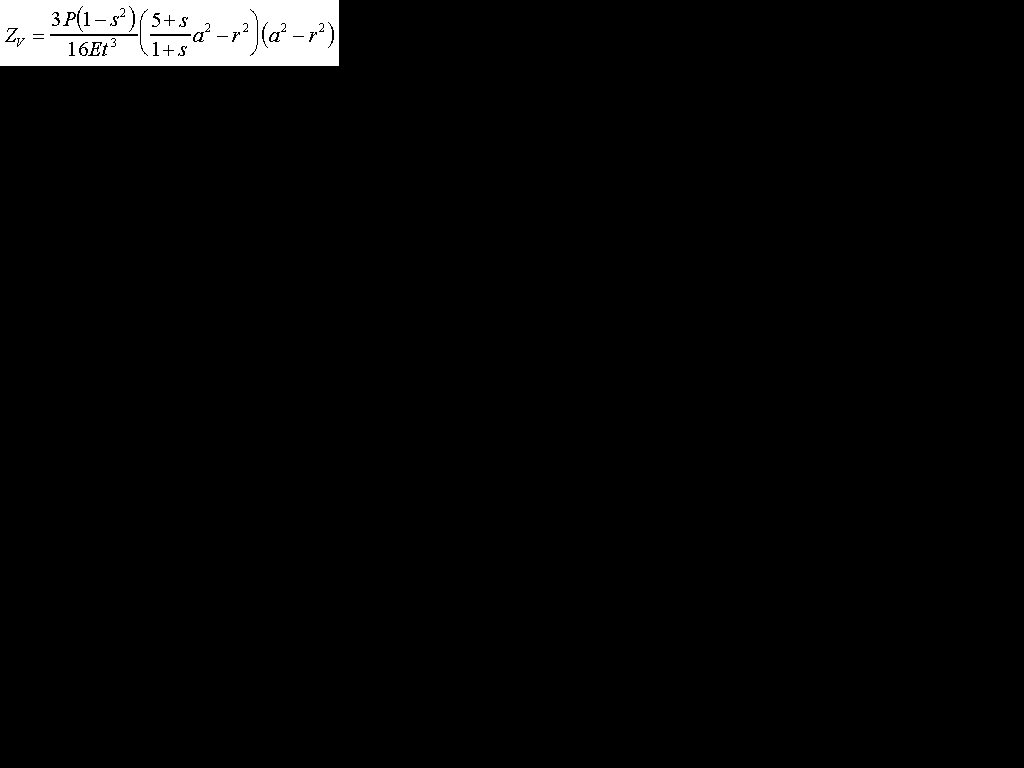
by Dave Rowe.
This section presents the development and practical use of the equations relating to vacuum pan deformation fabrication of Schmidt correctors.
The starting point for this discussion is the equation describing the deflection of a flat circular disk supported at its edge. The disk is not clamped and is uniformly loaded by a pressure difference between the front side and back side. The deflection of the disk is given by [1][2]:
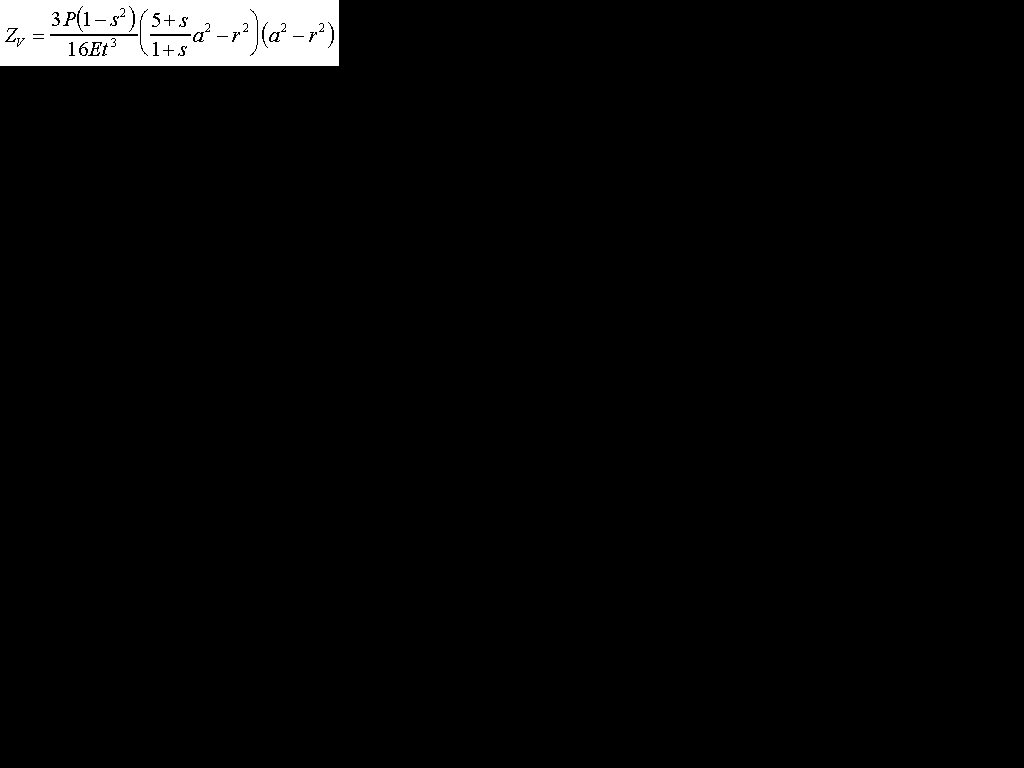 |
(1) |
Where Zv is the deflection of the disk, P = applied pressure difference, s = Poisson's ratio, E = Young's modulus, a= the radius of the disk, t = the thickness of the disk and r = the distance from the center of the disk to where the deflection, Zv, is measured. For glass, Poisson's ratio is between 0.21 and 0.25, so a reasonable value to use is 0.23. Letting Zc be the deflection of the center of the plate (at r=0), the above equation can be written as
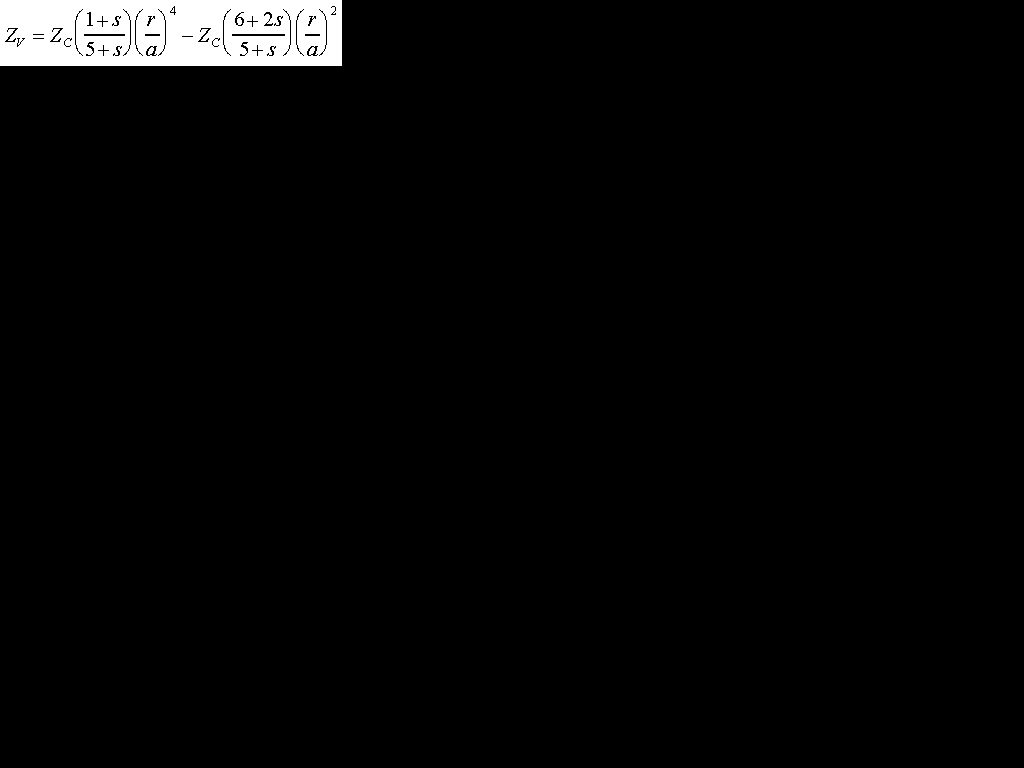 |
(2) |
where we have discarded the term with no dependence on r, and where
 |
(3) |
In the normal method of making a Schmidt corrector plate, a vacuum is pulled on the back side of the disk until the center deflection of the plate is Zc. Zc is determined by the required fourth-order coefficient of the corrector plate thickness and will depend on the optical system type, aperture and focal ratio. Therefore, equation (3) is only used to determining the pressure, P, required to deflect the plate, or in determining an appropriate thickness for the corrector plate, t, so that the pressure required is within a reasonable range. For glass, Young's modulus is between 7 and 10 million pounds per square inch (PSI).
Example: We wish to fabricate a corrector plate of 9.25" clear aperture and 0.25" thickness. How much pressure will be required to deflect the center of the plate by 2.6 mils? The vacuum pan is made with an inside diameter of 9.25". Using equation (3), and taking E= 8.5e6 PSI, s=0.23, a=4.625", t=0.25", we find that the pressure necessary for this deflection is P = 1.0 PSI which can be easily achieved by the lungs. Atmospheric pressure is about 14.7 PSI.
Returning to equation (2), we see that the deformed plate has a fourth-order deflection term, i.e., the surface height, Zv, has a term proportional to r to the fourth power. If we now grind and polish the surface flat, the corrector plate thickness would have a fourth-order component. This fourth-order term is under our control since we can pull as much vacuum as necessary to deflect the center by Zc. Looking at equation (2) we also see that when the plate is deformed there is a second order term in addition to the fourth-order term, i.e., a term that depends on r squared. If we ground the plate flat after deformation, this second order term would appear in the thickness of the corrector as a spherical component (a long radius sphere has a negligible fourth-order component). In a high quality optical system we must control both the second- and fourth-order components of the corrector thickness, so, instead of grinding the corrector plate flat after deformation, we grind and polish in a very shallow sphere. The radius of curvature of this sphere is under our control. In this way we can optimize both the second- and fourth-order terms of the thickness of the corrector plate.
Let S be the sagitta of the sphere that we grind and polish into the corrector plate while it is deformed. Then the thickness, Z, of the finished corrector plate will be given by:
 |
(4) |
Where T is a constant that describes the overall thickness of the blank. Combining this with equation (2) and removing terms that do not depend on r yields:
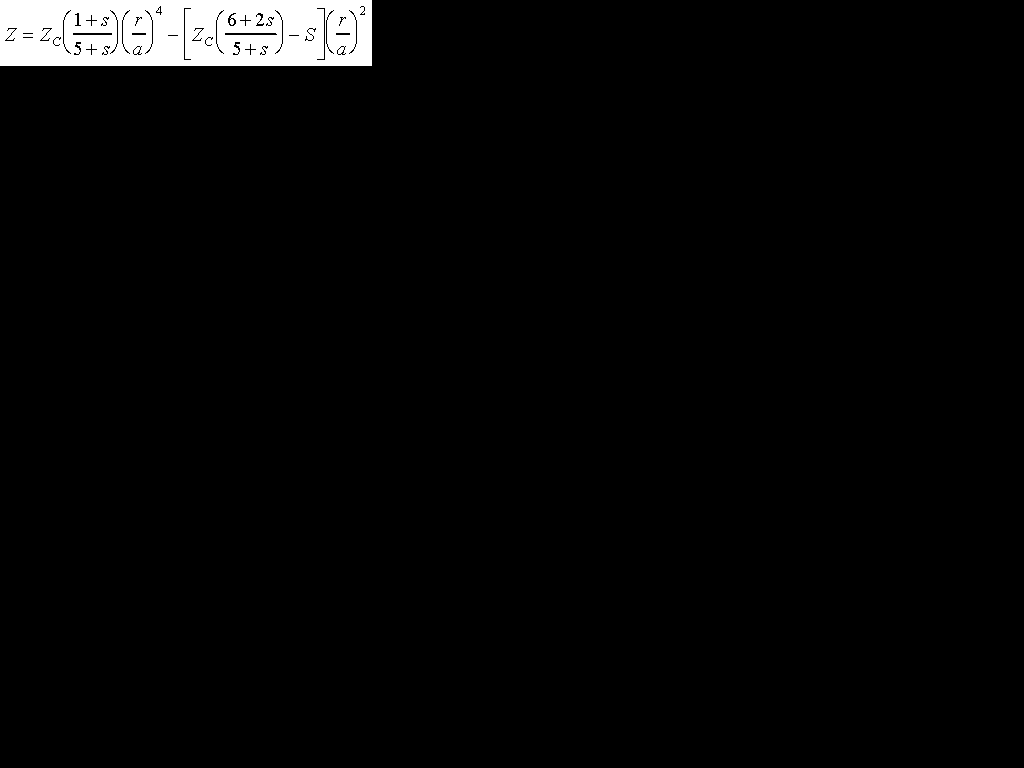 |
(5) |
This is the fundamental equation describing what happens to the corrector thickness when we deform it and then grind and polish in a sphere.
Now let's switch to the optical system for a moment. We assume that an optical system requiring a Schmidt corrector has been designed by either ray tracing or by mathematical analysis or both. This system requires a corrector plate that has a thickness profile given by:
(6) |
Equating coefficients in (5) and (6) we find:
 |
(7) |
Equations (7) are used to determine the amount of center deflection, Zc, of the plate under vacuum, and the sagitta, S, of the spherical tool used to grind the plate. If both sides of the plate are finish with the same (symmetrical) surface profile, then both S and Zc are divided by two after completing the calculation.
Example: A Schmidt corrector plate is desired with thickness profile given by A=9e-5, B=2.8e-6. The inside diameter of the vacuum pan is 9.25" (a=4.625"). Using equations (7), we have Zc=0.00545" and S=0.0048".
In many optical systems such as the Schmidt camera, the Wright telescope and the concentric Schmidt Cassegrain, the optical design has already been worked out. In this case, the corrector plate is characterized by a relative power, g, and the location of the neutral zone, D, which is given as a fraction of the radius of the corrector plate, i.e., if the neutral zone is at 85%, then D=0.85. Given g and D, the coefficients of the corrector thickness can be directly calculated from [3]:
 |
(8) |
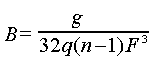 |
(9) |
where F is the focal length of the primary mirror, n is the index of refraction of the glass, q=1 if the correction is put on one side only and q=2 if the correction is put on both sides of the corrector plate. Note that when the correction is placed equally on both sides of the corrector, the values for A and B above are one half of those used when one side of the corrector is figured only. In practice, it is generally easier to figure both sides of the corrector plate because both sides must be ground and polished anyway.
Example: We wish to design a Wright telescope with a clear aperture of 40" having a focal ratio of 3 (a=20" and F=120"). BK7 optical crown glass is used for the corrector, having n=1.52. The neutral zone of the corrector is 86%, so D=0.86. The correction will be placed equally on both sides of the corrector plate so q=2. We find from Rutten and van Venrooij [4] that g=2.6 for our selected compact Wright telescope. Then equations (8) and (9) yield: A=2.68e-5, B=4.52e-8. Ray tracing confirms that these values yield a well corrected optical system. Now, using equations (7) we find that: Zc=30.75 mils, S=27.38 mils. Finally, we wish to select a corrector thickness that requires about 3 PSI to deflect the plate. Using equation (3) we find that t=1.12".
A Note on the Constants
by Steven de Haas
There is a table in the Encylopedia of Chemical Technology [5] giving Poisson's ratio and the modulus of elasticity for a lot of different types of glass. The type is designated by, for the most part, a four digit number. The modulus of elasticity ranges from 7e6 to 12e6 PSI. The number I would use, lacking better knowledge, is 10e6 PSI. Poisson's ratio ranges in this table from 0.16 to 0.28 and I would use 0.22. The way I arrived at these numbers was by eliminating the extremes and looking at what was left in terms of the number of times they occurred and taking an average. Of course, if you know the type of glass and its four digit number then you may be able to find more exact values in the stated reference.
Acknowledgements
I would like to thank Steven de Haas, Stuart Field and Bratislav Curcic for their help, suggestions and encouragement.References:
[1] Everhart, Applied Optics, vol. 5, p. 713 (1966).
[2] Theory of Plates
and shells, S. Timoshenko, McGraw-Hill NY 1940, page 62.
[3] Telescope
Optics, Evaluation and Design, by Rutten and van Venrooij, page 288.
[4]
ibid., page 124.
[5] Encyclopedia of Chemical Technology, Vol 12, John Wiley
and Sons, NY, 1994. ISBN 0-471-52681-9(V12). Pages 578-9.